翻译-高效的字符串匹配:辅助参考书目检索
原文地址:Efficient String Matching - An Aid to Bibliographic Search
作者 Alfred V. Aho,Margaret J. Corasick 贝尔实验室
本文为个人毕业设计外文参考文献翻译部分,有不当之处欢迎指正。
文章主要论述了 AC 自动算法的原理,函数构建,性能。(伪代码部分由于未能找到在代码块中插入数学符号的方式,故采用图片方式,若有相关方法,期待评论告知。)
本文描述了一种简单高效的算法,用于在文本字符串中找出任一有限字符数的关键词所有出现位置。这种算法通过关键词构建一个有限状态模式匹配机,然后通过这个模式匹配机在一趟遍历中处理单词输入的文本字符串。构建此模式匹配机的时间与关键字的长度之和成正比。通过模式状态匹配机处理文本字符串的状态转换次数与关键字的长度无关。这个算法已经将图书馆的参考书目搜索程序运行速度提升了 5 到 10 倍。
关键词:关键字和短语,字符串模式匹配,参考书目检索,信息检索,文本编辑,有限状态机,计算复杂度
CR类别:3.74,3.71,5.22,5.25
简介
在许多信息检索和文字编辑的应用程序中,能够在文本中快速定位用户指定的词或短语某些或者所有出现的位置是非常重要的。本文介绍了一种简单高效的算法,用于在任意的文本字符串中找出任一有限字符数的关键词或短语所有出现位置。
熟知有限自动机的人应该熟悉这种方法。这个算法由两部分组成。在第一部分中我们从关键词字符集中构造有限状态模式匹配机;在第二部分中我们将字符串作为模式匹配机的输入。只要这个机器已发现一个匹配的关键词,它就会发出信号。
在模式匹配程序中使用有限状态机并不新奇 [4,8,17],但程序员们似乎常常回避使用它们。部分程序员不愿意这样做的部分原因可能是因为从正则表达式 [3,10,15] 构建有限自动机的常规算法的复杂性,尤其是在需要最优解的情况下 [2,14] 。本文表明,从受限的正则表达式,也即由有限集合组成的关键词,可以快速而简单地构建一个高效的有限状态模式匹配机。我们的方法将有限状态机与 KMP 算法 [13] 相结合。
也许本文最有趣的地方在于有限状态算法提供了比常规方法更多的改进。我们在一个图书馆的参考书目查询程序中使用有限状态模式匹配算法。这个程序的目的是,让书目编者在引文索引中找到所有满足布尔匹配的关键词和短语的标题。这个查询程序开始是使用一种直接的字符串匹配算法。在该程序中使用有限状态算法来替代这个算法后,在典型输入上,运行时间为原程序的五到十分之一。
模式匹配机
本节描述了一种在文本字符串中定位关键词的有限状态字符串模式匹配机。下一节将描述从一个给定的有限关键字集合中构建类似机器的算法。
在本文中,字符串只是简单地表示为一个有限符号序列。设 \(K={y_1,y_2,\dots,y_k}\) 是一个有限字符串集合,我们称之为关键字,设 \(x\) 为任意字符串,我们称之为文本字符串。我们的问题是找出有限的所有x的子字符串中在K集合中的关键词。子字符串可能彼此重叠。
用于K的模式匹配机是一个程序,它将文本字符串 \(x\) 作为输入,关键字 \(K\) 在 \(x\) 的子字符串中的出现的位置作为输出。这种模式匹配机由一个状态集组成。每种状态都用一个数字表示。这种机器通过连续读取 \(x\) 中的字符来处理文本字符串 \(x\) ,产生状态转换,或是状态输出。这种状态机的行为由三个函数决定:一个跳转函数 \(g\) ,一个失败处理函数 \(f\) ,以及一个输出函数 \(output\) 。
图1展示了函数在模式匹配状态机针对关键字集 {he, she, his, hers} 时的使用情况。

一种状态(通常是 0 状态)被指定 \(start\) 状态。在图1中状态表示为 0,1,···,9。跳转函数 \(g\) 将一种状态和一个输入字符组成一对映射为一种状态或 \(fail\) 信息。图1(a) 的有向图表示跳转函数。例如,从 0 到 1 标有 h 的边表示 \(g(0,h) = 1\) 。没有箭头表示\(fail\)。因此,对于所有不是 e 或者 i 的输入字符 \(\delta\) , \(g(1,\delta)=fail\) 。我们的模式匹配机具有对所有的输入字符 \(\delta\) , \(g(0,\delta)\ne fail\) 的特性。我们将看到跳转函数在 0 状态的这个特性确保在每一个机器周期机器都将处理一个输入字符。
失败处理函数f将一个状态映射到另一个状态。当跳转函数返回 \(fail\) 时失败函数将被调用。当一组关键字被找到时,某些状态将被指定为输出状态。输出函数将一组关键字(可能为空)与每个状态组合将此形式化。
模式匹配机的一个操作周期定义如下:设 \(s\) 表示机器的当前状态, \(a\) 表示输入字符串 \(x\) 中的当前字符。
如果 \(g(s, a) = s’\),状态机执行跳转转换,进入状态 \(s’\) ,并将 \(x\) 的下一个字符作为当前输入字符。此外,如果 \(output(s’)\) 不为空,则机器输出 \(output(s’)\) 集合和当前输入字符的位置。这个操作周期现在已完成。
如果 \(g(s,a) = fail\) ,状态机调用失败函数 \(f\) ,也就是执行了失败转换。如果 \(f(s) = s’\) ,状态机重复以 \(s’\) 作为当前状态,以 \(a\) 作为当前输入字符的循环。
最初,状态机的当前状态为开始状态,文本字符串的第一个字符作为当前输入字符。状态机随后通过对每一个文本字符串的字符执行一个操作周期来处理文本字符串。
例如,考虑状态机 \(M\) 使用图1 中的函数处理文本字符串 “ushers” 的行为。图2表明了 \(M\) 处理文本字符串的状态转换关系。
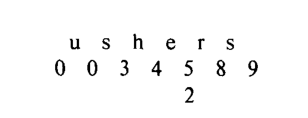 考虑这样一个操作周期, \(M\) 处在状态 4,当前输入字符为 e 。因为
\(g(4,e) = 5\) ,状态机进入状态
5,前移到下一个输入字符,并输出 \(output(5)\)
,表明状态机已经发现了在文本字符串的倒数4个位置是关键词 “she” 和 “he”
。
考虑这样一个操作周期, \(M\) 处在状态 4,当前输入字符为 e 。因为
\(g(4,e) = 5\) ,状态机进入状态
5,前移到下一个输入字符,并输出 \(output(5)\)
,表明状态机已经发现了在文本字符串的倒数4个位置是关键词 “she” 和 “he”
。
在状态 5输入字符 r,状态机在它的操作周期中执行两次状态转换。因为 \(g(5,r) = fail\) , \(M\) 进入状态 \(2 = f(5)\) 。然后因为\(g(2,r) = 8\),\(M\) 进入状态 8,接着前移一个输入字符。在这个操作周期中没有产生输出。
以下算法总结了模式匹配机的行为。
算法1 模式匹配机
输入 一个文本字符串 \(x = a_1a_2 \dots a_n\) ,每一个 \(a_i\) 作为一个输入字符,模式匹配机 \(M\) 包含跳转函数 \(g\),失败函数 \(f\),以及输出函数 \(output\),如上所述
输出 关键词在\(x\)中的位置
方法

每一趟for循环都代表状态机的一个操作周期。
算法1是在 KMP 算法的基础上模式化得到的,KMP 算法用于在一个文本字符串中查找一个关键字 [13],也可以看作是 [11] 中讨论的 “trie” 搜索方法的扩展。Hopcroft和Karp(当时未发表)提出一种类似于算法1的模式,用于在文本字符串中查找任一有限关键字集合第一次出现的位置 [13]。本文的第6节探讨了一种算法1的有限自动机版本,它避免了所有的失败转换。
构造跳转,失败,输出函数
我们说,当 \(g,f,output\) 三个函数应用于一组关键字,算法1表现为,关键字 \(y\) 在文本字符串 \(x\) 的第 \(i\) 个位置中止,当且仅当 \(x= uyv\) 并且\(uy\)的长度为 \(i\)。
现在我们应该展示如何从一个关键字集构建有效的跳转,失败和输出函数。构建分为两部分。第一部分我们定义状态和跳转函数。第二部分我们计算失败函数。输出函数的计算则在第一部分开始构建,在第二部分完成。
为了构建跳转函数,我们应该构建一个跳转图。我们从一个表示状态 0 的顶点开始这幅图。然后我们通过往图中添加一条从开始状态引出的有向路径将关键字 \(y\) 添加到图中。这样就会有新的顶点和边被添加到图中,从开始状态开始,一条路径拼出关键字 \(y\)。当一个状态终结了这条路径,关键字 \(y\) 将被添加到输出函数中。我们仅在必要时才往图中添加新的边。
例如,设 {he,she,his,hers} 是关键字集。将第一个关键字添加到图中,我们得到:
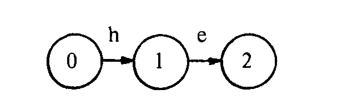
从0到2的路径拼出了关键字 “he”;我们将输出 “he” 关联到状态2.添加第二个关键字 “she”,我们得到图:
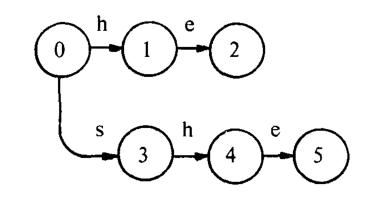
输出 “she” 被关联到状态 5。添加关键字 “his”,我们得到下面的图。注意到,当我们添加关键字 “his” 时,已经有从状态 0 到状态 1 标号为 “h” 的边,所以我们不需要添加另一条从状态 0 到状态 1 标号为 “h” 的边。输出 “his” 被关联到状态 7。
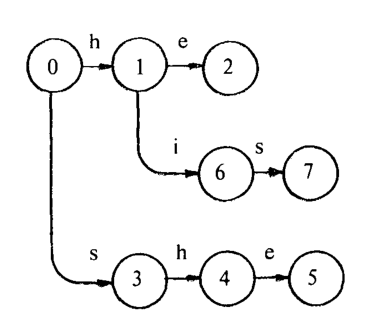
添加最后一个关键字 “hers”,我们得到:
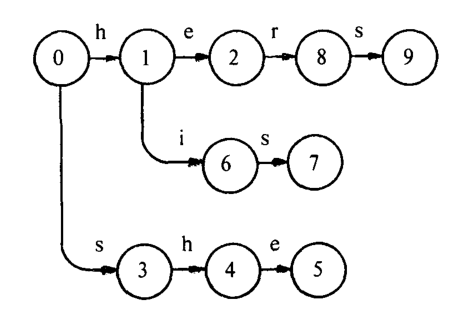
输出 “hers” 被关联到状态 9。这时我们可以使用已经存在的从状态 0 到状态 1 标号为 “h” 的边和从状态 1 到状态 2 标号为 “e” 的边。
到目前为止,这幅图是一棵有根的有向树。为了完成跳转函数的构建,我们为所有不是 “h” 或 “s” 的输入字符添加一个从状态 0 到状态 0 的循环。我们得到了一个如图1(a)所示的有向图。这幅图表示跳转函数。
失败函数从跳转函数构建。不妨设状态\(s\)的深度为在跳转图中从开始状态到 \(s\) 的最短路径。这样在图1(a)中,开始状态的深度为 0,状态1和状态3深度为1,状态2,4,6深度为2,以此类推。
我们应该计算失败函数中所有深度为 1 的状态,所有深度为 2 的状态,以此类推,直到失败函数计算了所有的状态(除了在失败函数中未定义的状态 0)。这个算法从理论上通过状态来计算失败函数 \(f\) 非常简单。我们令所有深度为1的状态 \(f(s)=0\)。现在假设所有深度小于 \(d\) 的状态的 \(f\) 都已被计算,深度为\(d\)的状态的失败函数值将从深度小于 \(d\) 的状态的失败函数值来计算。深度为 \(d\) 的状态可以从深度为 \(d-1\) 的状态的跳转函数定义。
特别地,为了计算深度为 \(d\) 的状态的失败函数,我们考虑深度为 \(d-1\) 的每个状态\(r\),按照如下步骤进行:
如果对所有 \(a\),\(g(r,a) = fail\),不执行任何操作
否则,对于每个字符 \(a\),\(g(r,a) = s\),执行如下操作:
令 \(state = f(r)\)
执行语句 \(state\leftarrow f(state)\) 零至多次,直到有一个状态的值满足 \(g(state,a)\ne fail\)。(注意因为对于所有的输入 \(a\),\(g(0,a)\ne fail\),因此满足条件的状态总是可以找到。)
令 \(f(s) = g(state,a)\)
例如,为了计算图1(a)中的失败函数,我们将首先令 \(f(1) = f(3) = 0\),因为状态1和3的的深度为1。之后我们来计算深度为2 的状态2,6,4。为了计算\(f(2)\),我们令 \(state=f(1) = 0\);接着因为 \(g(0,e) = 0\),我们得到 \(f(2) = 0\)。为了计算 \(f(6)\),我们令 \(state = f(1) = 0\);而因为 \(g(0,i) = 0\),我们得到 \(f(6) = 0\)。为了计算 \(f(4)\),我们令 \(state = f(3) = 0\);又因为 \(g(0,h) = 1\),我们得到 \(f(4) = 1\)。继续这个方法,我们得到图1(b)中所示的失败函数表。
在计算失败函数时,我们同时更新输出函数。当我们确认 \(f(s) = s’\) 时,我们将状态 \(s\) 的输出与状态 \(s’\) 的输出归并。
例如,在图1(a)中我们定义 \(f(5) = 2\)。此时我们归并状态2的输出集,也即 {he},加上状态5的输出及得到新的输出集 {he,she}。最后非空的输出及如图1(c)所示。
这个从\(K\)集合构建了跳转,失败和输出函数的算法小结如下。
算法2 跳转函数构建
输入 关键字集\(K={y_1,y_2,\dots,y_k}\)
输出 跳转函数 \(g\) 和部分输出函数的计算值
方法 我们假设当状态 \(s\) 开始被创建时 \(output(s)\) 为空,以及当 \(a\) 未定义或 \(g(s,a)\) 尚未被定义时,\(g(s,a) = fail\)。过程 \(enter(y)\) 往跳转图中插入一条拼写为 \(y\) 的路径。
上面的算法,内循环与算法1类似,计算失败函数值。

算法3 构建失败函数。
输入 算法2中的跳转函数 \(g\) 和输出函数 \(output\)。
输出 失败函数 \(f\) 和输出函数 \(output\)。
方法

第一个 for 循环计算深度为1的状态并将它们记录在一个先入先出的可变队列表示的表中。 while 主循环从深度为 \(d-1\) 的状态集中计算深度为 \(d\) 的状态集。
算法3所产生的失败函数值在下面的情况下可能并非最佳。考虑图1中的模式匹配机 \(M\) ,我们看到 \(g(4,e) = 5\)。如果 \(M\) 在状态4并且当前输入字符 \(a_i\) 不是 e,那么 \(M\) 将进入状态 \(f(4) = 1\)。因为 \(M\) 已经认定 \(a_i\ne e\),于是 \(M\) 无需考虑跳转函数在输入为 e 时状态1的值。实际上,如果关键字 “his” 不存在,\(M\) 将直接从状态4到状态0,跳过一个并非必要的中间转换状态1。
为了避免不必要的失败转换我们可以使用 \(f’\) 概括[13]中的下一个函数取代算法1中的 \(f\)。特别地,令 \(f’(1)=0\)。对于 \(i\) 大于1的情况,定义 \(f’(i) = f’(f(i))\),因此对于所有的输入字符 \(a\),\(g(f(i),a)\ne fail\) 即 \(g(i,a)\ne fail\);否则令 \(f’(i) = f(i)\)。但是,为了避免任何失败转换,我们可以使用第6节介绍的算法1的确定有限自动机版本。
算法1,2,3的性质
本节证明从一个给定的关键字集合 \(K\) 同通过算法2和算法3来构建跳转函数,失败函数和输出函数确实有效。
我们设字符串 \(uv\) 的 \(u\) 为前缀,\(v\) 为后缀。如果 \(u\) 不是一个空字符串,那么 \(u\) 是一个合法的前缀,同样地,如果 \(v\) 非空,那么 \(v\) 是一个合法的后缀。
我们设字符串 \(u\) 表示在模式匹配机中的跳转图中从开始状态到状态\(s\)的最短路径所拼出的字符。开始状态用空字符串表示。
我们的第一个引理表示通过算法3构建的失败函数。
引理1 假定跳转图中状态 \(s\) 由字符串 \(u\) 表示,而状态 \(t\) 由字符串 \(v\) 表示。那么,\(f(s)=t\) 当且仅当 \(v\) 是 \(u\) 的最长合法后缀,是某个关键词的前缀。
证明 证明通过对 \(u\) 的长度(或者也可以说状态\(s\)的深度)进行归纳法达成。在算法3中,\(f(s)=0\) 的所有状态深度为1。既然每个深度为1的状态都由一个长度为1的字符串所代表,引理对所有的长度为1的字符串成立。
归纳的下一步,假设引理1的叙述对所有长度小于 \(j(j>1)\) 的字符串为真,令 \(u=a_1a_2\dots a_j\) ,对于部分大于1的 \(j\),\(v\) 是 \(u\) 最长的合法后缀,是一些关键字的前缀。假设\(u\)代表状态 \(s\) 而 \(a_1 a_2\dots a_{j-1}\) 代表状态 \(r\)。状态队列 \(r_1,r_2,\dots,r_n\) 会像是:
\(r_1 = f(r)\)
\(r_{i+1} = f(r_i)(1\le i<n)\)
\(g(r_i,a_j) = fail(1\le i<n)\)
\(g(r_n,a_j) = t \ne fail\)
(如果 \(g(r_1,a_j)\ne fail\),那么 \(r_n = r_1\)。)队列 \(r_1,r_2,\dots,r_n\) 是算法3中的 while 内循环的可变状态的假设值队列。while 循环的上述描述使得 \(f(s) = t\)。我们定义 \(t\) 由 \(u\) 的最长合法后缀表示,同时也是一些关键字的前缀。
为了证明这点,假设 \(v_i\) 表示状态 \(r_i(1\ne i\ne n)\)。通过归纳假设,\(v_1\) 是 \(a_1 a_2 \dots a_{j-1}\) 的最长后缀,是某些关键字的前缀;\(v_2\) 是 \(v_1\) 的最长后缀,是某些关键词的前缀;\(v_3\)是\(v_2\)的最长后缀,是某些关键词的后缀,以此类推。
现在 \(v_n\) 是 \(a_1a_2\dots a_{j-1}\) 的最长合法后缀,\(v_na_j\) 是一些关键字的前缀。因此 \(v_na_j\) 是 \(u\) 的最长后缀,同时是也些关键字的前缀。根据算法3有 \(f(s)=g(r_n,a_j)=t\) ,证毕。
下一条引理证明通过算法2和算法3构建的输出函数。
引理2 \(output(s)\) 集合有且仅有包含一个关键字,同时也是代表状态\(s\)的后缀字符串。
证明 在算法2中无论我们何时向跳转图中添加一个状态 \(s\) ,它都由我们通过 \(output(s)={y}\) 得到的关键字 \(y\) 表示。给定这个初值,我们可以演示关于状态 \(s\) 的深度的推演,\(output(s) ={y|y\text{是一个表示状态}s\text{的后缀字符串关键字}}\)。
这个描述对于深度为0的开始状态是绝对正确的。假定这个叙述对于所有深度小于 \(d\) 的状态为真,考虑深度为 \(d\) 的状态 \(s\)。我们用字符串 \(u\) 代表状态 \(s\)。
考虑在 \(output(s)\) 中的一个字符串 \(y\)。如果 \(y\) 是通过算法2添加到 \(output(s)\) 中的,那么 \(y=u\),且 \(y\) 是一个关键字。如果 \(y\) 是通过算法2添加到 \(output(s)\) 中的,那么 \(y\) 在 \(output(f(s))\)中。通过归纳假设,\(y\) 是一个关键字,同时是一个代表状态 \(f(s)\) 的字符串的后缀。根据引理1,任一这样的关键字必须有一个 \(u\) 的后缀。
反过来,假设 \(y\) 是任一关键字,同时是 \(u\) 的后缀。因为 \(y\) 是一个关键字,又状态 \(t\) 由 \(y\) 表示,根据算法2,\(output(t)\) 包含 \(y\)。因此如果 \(y=u\),那么 \(s=t\) 并且 \(output(t)\) 中包含\(y\)。如果 \(y\) 是 \(u\) 的一个合法后缀,那么从归纳假设和引理1我们知道 \(output(f(s))\) 包含 \(y\)。因为算法3从增长的深度来考虑状态,算法3的最后一条语句添加 \(output(f(s))\),因此 \(y\) 在 \(output(s)\) 中。
下面这条引理表示算法1在一个文本字符串 \(x=a_1a_2\dots a_n\) 上的行为。
引理3 在第 \(j\) 个操作周期之后,当且仅当表示 \(s\) 的 \(a_1a_2\dots a_j\) 最长后缀是某个关键词的前缀时,算法1会处在 \(s\) 状态。
证明 和引理1类似。
定理1 算法2和算法3产生有效的跳转,失败,和输出函数。
证明 通过引理2和引理3。
算法1,2,3的时间复杂度
现在我们考查算法1,2,3的时间复杂度。我们会证明使用通过算法2和算法3创建的跳转,失败和输出函数,在处理一个文本字符串时,由算法1导出的状态转化数量与关键字数量无关。我们还将证明算法2和算法3在处理时间上可以达到与 \(K\) 中的关键字的总长度成线性比例。
定理2 使用通过算法2,算法3和算法1构造的跳转,失败和输出函数处理一个长度为 \(n\) 的文本字符串可以让状态转换次数小于 \(2n\)。
证明 在算法1的每一个操作周期中通过一个跳转函数制造0次或者更多的失败转换。从一个深度为\(d\)的状态\(s\),算法1永远不会在一个操作周期中制造多于\(d\)次的失败转换(作者注:最多可以达到\(d\)次失败转换,[13]证明,如果\(K\)中仅有一个关键字,在一个操作周期中,失败转换次数的最大值是 \(O(log d)\))。那么总的失败转换次数一定最少比总的跳转转换次数少1.在处理一个长度为 \(n\) 的输入时,算法1恰好进行\(n\)次跳转转换。因此总的转换次数小于 \(2n\)。
算法1的实际时间复杂度取决于它有多繁杂:
对于每个状态 \(s\) 和输入字符 \(a\),确定 \(g(s,a)\)
对于每个状态 \(s\),确定 \(f(s)\)
确定 \(output(s)\) 是否为空
输出 \(output(s)\)
我们可以将跳转函数值存储在一个二维数组中,它将允许我们在常数时间内对于每一组 \(s\) 和 \(a\) 确定 \(g(s,a)\) 的值。如果输入字母表的长度和关键字集较大,那么可能对于每个状态仅在一个线性表[1,11]中存储不合格的值要合理得多。这样的处理将使取决于 \(g(s,a)\) 的复杂度变为状态 \(s\) 在跳转函数中不合格值的数量。一个合理的折中,也是我们使用的,是将最频繁使用的状态(例如状态0)存储在直接存取表中,下一个状态可以通过当前输入字符在表中的直接索引来定位。对于最频繁使用的状态,我们可以在常数时间内对每一个 \(a\) 确定 \(g(s,a)\)。较少使用的状态和跳转函数值为不合格的状态可以编码在线性表中。
另一个方法会将每一个状态的跳转值以二叉树的形式存储。
失败函数值可以存储在一维数组中,这样对于每一个 \(s\) 可以在常数时间内确定 \(f(s)\)。
算法1中未打印的部分可以用于在 \(cn\) 步内处理长度为 \(n\) 的文本字符串,\(c\) 是一个与关键字数量无关的常数。
现在我们考虑需要打印的输出次数。可以使用一个一维数组在常数时间内确定 \(output(s)\) 是否为空。在每一个操作周期中,打印输出花费的时间正比于 \(output(s)\) 中关键字的长度总和,\(s\) 是算法1 在每个操作周期中的结束状态。在许多情况下,\(output(s)\) 通常只有一个关键字,所以对于每个输入状态打印输出所需的时间是常数。
然而,数量众多的关键词集可能出现在文本字符串的每个位置。在这种情况下算法1将会花费相当大的时间来打印输出结果。在最坏的情况下我们可能不得不打印\(K\)中的所有关键字,简直是文本字符串的每个位置。(考虑一个极端情况,\(K = {a,a^2,a^3,\dots,a^k}\),文本字符串是 \(a^n\)。即 \(a_i\) 是 \(i\) 个 \(a\) 的字符串。)任何其他的模式匹配机算法将不得不打印所有在文本字符串的每个位置打印同样数量的关键字,所以,比较模式匹配算法在使用时间的基础上识别关键字出现的位置是合理的。
我们应该比较算法1与另一种更直接的方式的表现,这种方式定位 \(K\) 中的所有是给定的文本字符串的子串的位置。这样的方式将会返回每一个 \(K\) 中的关键字,并针对文本字符串的所有字符位置成功匹配关键字。这种方法的运行时间最多与\(K\)中关键字的数量乘以文本字符串的长度成比例。如果有许多的关键字,算法性能将会比算法1差得多。实际上,正是早前算法的时间复杂度促使了算法1的发展。(读者可能希望在以下情况比较以下两个算法的性能,\(K = {a,a^2,a^3,\dots,a^k}\),文本字符串是 \(a^n\)。)
定理3 算法2所需时间与关键字的总长度成线性比例关系。
证明 前面已证明。
定理4 算法3对关键字的总长度处理可以达到线性级别。
证明 使用与定理2类似的方法,我们可以证明状态语句 \(state\leftarrow f(state)\) 执行的总次数超出了关键字的总长度。使用链表来表示一个状态的输出集,我们可以在常数时间内执行语句 \(output(s)\leftarrow output(s)\cup output(f(s))\)。注意当语句执行时 \(output(s)\) 和 \(output(f(s))\) 是不相关的。因此使用算法3所需的总时间主要取决于关键字的总长度。
消除失败转换
本节展示如何在算法1中使用下一个函数到一个在跳转函数和失败函数的确定有限自动机位置来消除失败转换。
一个确定有限自动机[15]包括一个有限状态集 \(S\) 和一个下一步转移函数 \(\delta\),对于每个状态 \(s\) 和输入字符 \(a\),\(\delta(s,a)\) 是 \(S\) 中的一个状态。也就是说,一个确定有限自动机使状态转换和每个输入字对应。
通过在算法1中的跳转函数合适的地方在一个合适的有限自动机中使用下一步转移函数 \(\delta\),我们可以分配所有的失败转换。这很容易通过替换算法1的for循环中前两句语句为一条语句 \(state\leftarrow \delta(state,a_i)\)。使用 \(\delta\),算法1完全做到每个输入字符一个状态转换。
我们可以计算通过算法2,3,4建立的跳转和失败函数所需的下一步转换函数 \(\delta\)。算法4对每一个队列中的可能失败转换做了计算。算法4所需的时间与关键字集的大小呈线性相关。实际上,算法4会在算法3中被评估。
下一步转换函数计算通过算法4计算图1中展示的和图3中列表的跳转函数和失败函数。
下一步转换函数在图3中的编码如下。例如,在状态0中,我们有一个到状态1的转换 h,一个到状态3的转换 s,和一个到状态0的任一字符表示的状态。在每一个状态中,点表示任一上面其他的输入字符。这种下一步跳转函数的编码函数比将 \(\delta\) 存储为一个二维的数组更经济。但是以这种方式存储 \(\delta\) 所需的内存大于相应的 \(\delta\) 函数所构建的跳转函数,因为在 \(\delta\) 中的许多状态,每一个都包含来自很多跳转函数的状态转换。
在图3中使用下一步跳转函数,算法1在输入为 “ushers” 时将会产生如图2第一行状态所示的状态转换。
在算法1中使用一个确定的有限自动机很可能将状态转换数量减少50%。但理论上节省的开销未必在实践中能达到,因为在典型案例中算法1将花费大多数实践中没有失败转换的状态0上。但是计算预期节省的开销是困难的,因为无法定义有意义的平均关键字集和平均文本字符串。
算法4 构造一个确定有限自动机
输入 算法2的跳转函数 \(g\) 和算法3的失败函数 \(f\)
输出 下一步输出跳转函数 \(\delta\)
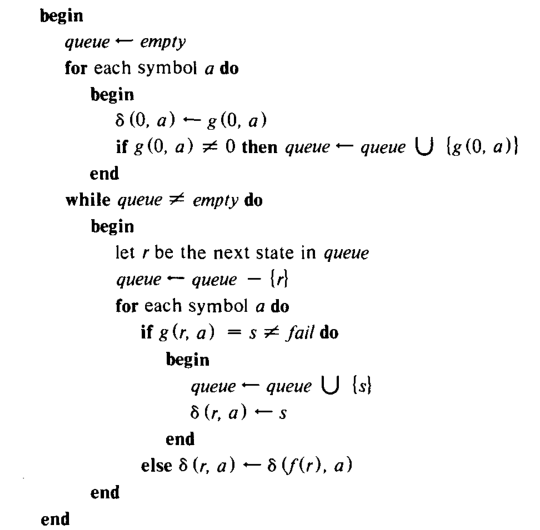

在参考书目检索中的应用
算法1在模式匹配应用于大规模关键字时很有优势,因为所有的关键字在文本字符串中同时匹配只需要遍历一次文本字符串。这种算法类似的应用已经成功被用于一个图书馆参考书目检索程序中,用于定位在所有的参考书目中找到满足一定关键字布尔函数的所有参考书目。
这个检索系统所使用的数据库是贝尔实验室的技术图书库中用于当代科技论文的机器可读数据。这些参考书目来自期刊,覆盖了很广阔的技术领域。在1973年夏天,三年累积的数据,覆盖了大概150000条参考书目,总长度约有107个字符。
使用这个搜索系统书目编者可以在数据库中找到所有标题满足布尔组合条件的关键字。例如,书目编者可以请求查找数据库中所有同时包含关键字 “ion” 和 “bombardment” 的条目。书目编者也可以指定一个关键字是否有优先词 and/or,以及一些标点符号例如空格,逗号,分号等等。指明特性可以精确排除嵌于文本中的关键字。例如,将 “ions” 视为子串 “ion” 的匹配结果通常是合理的。但是,将 “motions” 视为该关键词的匹配结果通常就不合理了。这种实践允许选择接收完全嵌入的情况,左包含,右包含,或者不允许包含。这条规定对于算法1来说完全没有难度,即使用于标点符号在大量的跳转转换的关键词语法创造的状态。这可能导致算法1的确定有限自动机的应用消耗更多的空间,从而对一些应用来说失去魅力。
这个参考书目搜索程序的一个早期版本引进了一个直接的模式匹配算法,每个关键词在搜索指令中成功匹配每个标题。这个程序的第二个版本被投入使用,也是使用 FORTRAN 语言,不同之处仅仅在于模式匹配模式在算法1,2,3的子情况。下面的表格展示了两个样本运行在Honeywell 6070电脑中的两个程序的情况。第一个搜索样本包含15个关键字,第二个搜索样本包含24个关键字。(计算时间开销如下表所示)
| 15个关键字 | 24个关键字 | |
|---|---|---|
| 旧系统 | 0.79 | 1.27 |
| 新系统 | 0.18 | 0.21 |
越大的关键字集性能的改善更明显。数据表明算法1的搜索开销几乎与关键字的数量相独立。构建模式匹配机和状态转换的时间开销与读取和输出文本字符串的时间开销微不足道。
结束语
本文阐述了模式匹配的有效应用,我们在文本字符串中查找大量的关键字的位置。因为没有额外的信息需要添加到文本字符串中,搜索可以跨任意文件。
一些信息查找系统计算一个文本文件的索引或者词语注解索引,使得搜索可以无需扫描整个文本字符串来进行[7]。在此类系统中改变文本文件很奢侈,因为每一处更改之后文件索引也必须更新。因此,此类系统最好用于长期静态的文本文件以及简短的模式。
有限自动机理论中一个有趣的问题是:给定一个长度为\(r\)的正则表达式 \(R\) 和一个长度为 \(n\) 的字符串 \(x\),在 \(R\) 中找到 \(x\) 可以多快?解决这个问题的一种方法是从 \(R\) 构建一个并非确定的有限自动机 \(M\) 然后模拟 \(M\) 输入 \(x\) 时的行为。这种方案的时间复杂度为 \(O(r n)\)。
另一种方式循着正则表达式去构建一个不确定的有限自动机 \(M\),然后将 \(M\)转化为一个确定的有限自动机 \(M’\) 并且使用 \(M’\) 模拟输入 \(x\) 时的行为。这种方法的唯一难处在于\(M\)可能有 \(2^r\) 种状态顺序。当然另一方面 \(M’\) 的仿真是线性的。总体的时间复杂度为 \(O(2^r+n)\)。
我们可以使用算法4从一个正则表达式\(R\)直接构建一个确定有限自动机,所需时间与R的长度呈线性关系。但是,正则表达式的形式目前仅限为 \(\Sigma*(y_1 + y_2 + \dots + y_k)\Sigma*\) ,\(\Sigma\) 是输入字符表。通过一系列确定有限自动机的前后级联,我们可以将正则表达式扩充为 \(\Sigma*Y_1\Sigma*Y_2\dots \Sigma*Y_m\Sigma*\) 的形式,\(Y_i\)是一个形式为\(y_{i1} + y_{i2} +\dots+ y_{ik_i}\)的正则表达式。
一个相关的开放性问题是新型常规集可以在少于\(O(rn)\)的时间内被识别出。[5]中表明循着这种方式具有形式为 \(\Sigma*y\Sigma*\) 的正则表达式( \(y\) 是关键字“don’t care”字符)可以在 \(O(n log r log log r)\) 时间内被识别出。
致谢
作者们感谢A.F.Ackerman,A.D.Hall,S.C.Johnson,B.W.Kernighan,以及M.D.McIlroy对手稿的有帮助的意见。本文使用Kernighan和Cherry[9]创制的排版设置。感谢B.W.Kernighan以及M.E.Lesk在准备这篇文论时的帮助。
1974年8月收到;1975年1月修订
参考文献
Aho, A.V., Hoperoft, J.E., and Ullman, J.D. The Design and Analysis of Computer Algorithms. Addison-Wesley, Reading, Mass., 1974.
Booth, T.L. Sequential Machines and Automata Theory. Wiley, New York, 1967.
Brzozowski, J.A. Derivatives of regular expressions. J. ACM 11:4 (October 1964), 481-494.
Bullen, R.H., Jr., and Millen, J.K. Microtext - the design of a microprogrammed finite state search machine for full-text retrieval. Proc. Fall Joint Computer Conference, 1972, pp. 479-488.
Fischer, M.J., and Paterson, M.S. String matching and other products. Technical Report 41, Project MAC, M.I.T., 1974.
Gimpel, J.A. A theory of discrete, patterns and their implementation in SNOBOL4. Comm. ACM 16:2 (February 1973), 91-100.
Harrison, M.C. Implementation of the substring test by hashing. Comm.ACM14:12 (December 1971), 777-779.
Johnson, W.L., Porter, J.H., Ackley, S.I., and Ross, D.T. Automatic generation of efficient lexical processors using finite state techniques. Comm. ACM 11:12(December 1968), 805-813.
Kernighan, B.W., and Cherry, L.L. A system for typesetting mathematics. Comm. ACM 18:3 (March 1975), 151-156.
Kleene, S.C. Representation of events in nerve nets. In *Au**tomata Studies,* C.E. Shannon and J.McCarthy (eds.), Princeton University Press, 1956, pp. 3-40.
Knuth, D.E. Fundamental Algorithms, second edition, The Art of Computer Programming 1, Addison-Wesley, Reading, Mass.,1973
Knuth, D.E. Sorting and Searching, The Art of Computer Programing 3, Addison-Wesley, Reading, Mass., 1973.
Knuth, D.E., Morris, J.H., Jr., and Pratt, V.R. Fast pattern matching in strings. TR CS-74-440, Stanford University, Stanford, California, 1974.
Kohavi, Z. Switching and Finite Automata Theory. McGraw-Hill, New York, 1970.
McNaughton, R., and Yamada, H. Regular expressions and state graphs for automata. IRETrans. Electronic Computers 9:1 (1960), 39-47.
Rabin, M.O., and Scott, D. Finite automata and their decision problems. IBM J. Research and Development 3, (1959), 114-125.
Thompson, K.Regular search expression algorithm. Comm. ACM 11:6 (June 1968), 419-422.