算法-二分搜索算法

发表于 更新于 分类于

算法：二分搜索算法（折半查找算法） 时间复杂度：\(O(log \; n)\)

  • 二分搜索算法概述
  • 二分搜索算法伪代码
  • 二分搜索算法实现

二分搜索算法概述

二分搜索算法，也称折半查找算法，即在一个有序数组中查找某一个特定元素。整个搜索过程从中间开始，如果要查找的元素即中间元素，那么搜索过程结束；反之根据中间元素与要查找元素的关系在数组对应的那一半查找，例如查找元素大于中间元素，则在整个数组较大元素的那一半查找，反复进行这个过程，直到找到元素，或者数组为空，查找不到元素。

这里有一张非常形象的算法描述图：

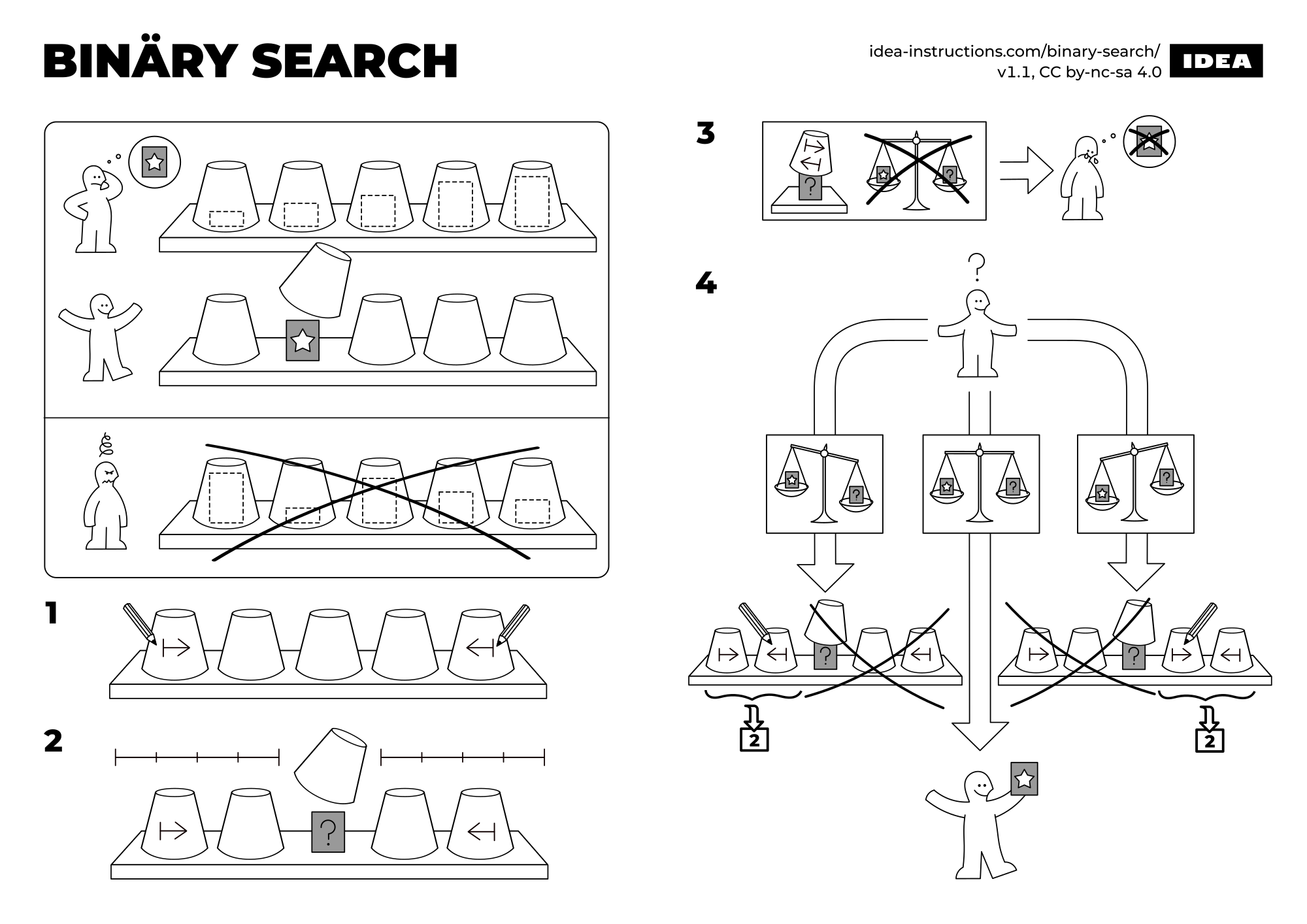
Binary Search

二分搜索算法描述

给定一个数组 \(A_0, A_1... A_{n-1}\)， \(A_0 \le A_1 \le \cdot \le A_{n - 1}\)，待查找元素为searchnum：

  1. 用left，right分别表示左右端点，即要查找的范围；
  2. 用middle表示中间点，\(middle = \lfloor (left + right) / 2 \rfloor\)；
  3. 若left > right，搜索失败；
  4. 若 \(A_{middle}\) >searchnum，right = middle - 1，返回3；
  5. 若 \(A_{middle}\) < searchnum，left = middle + 1，返回3；
  6. 若 \(A_{middle}\) = searchnum，搜索结束，返回middle。

二分搜索算法伪代码

BINARY-SEARCH-WHILE(A, searchnum, left, right) 

1
2
3
4
5
6
7
while left <= right
  middle = (left + right) div 2
  case
    A_middle < searchnum : left = middle + 1
    A_middle > searchnum : right = middle - 1
    A_middle = searchnum : return middle
return FAILED

BINARY-SEARCH-RECURSION(A, searchnum, left, right) 

1
2
3
4
5
6
7
8
9
if left <= right
  middle = (left + right) div 2
  case
    A_middle < searchnum :
      return (A, searchnum, middle + 1, right)
    A_middle > searchnum :
      return (A, searchnum, left, middle - 1)
    A_middle = searchnum :
      return middle

二分查找算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int binarySearch(arrType * a, arrType searchnum, int left, int right)
{
    int middle;
    while (left <= right) {
        middle = (left + right) / 2;
        if (a[middle] > searchnum)
            right = middle - 1;
        else if (a[middle] < searchnum)
            left = middle + 1;
        else if (a[middle] == searchnum)
            return middle;
    }
    return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int binarySearch(arrType * a, arrType searchnum, int left, int right)
{
    int middle;
    if (left <= right) {
        middle = (left + right) / 2;
        if (a[middle] > searchnum)
            return binarySearch(a, searchnum, left, middle - 1);
        else if (a[middle] < searchnum)
            return binarySearch(a, searchnum, middle + 1, right);
        else if (a[middle] == searchnum)
            return middle;
    }
    return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 外部定义全局变量：
var
    a : array[1..n] of integer;
    searchnum, result :integer;

procedure binarySearch(left, right :integer);
var
    middle : integer;
begin
    while (left <= right) do
        begin
            middle := (left + right) div 2;
            if (a[middle] > searchnum) then
                right := middle  - 1
            else if (a[middle] < searchnum) then
                left := middle + 1
            else
                begin
                    result := middle;
                    break;
                end;
        end;
    if left > right then
        result := -1;
end;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 外部定义全局变量：
var
    a : array[1..n] of integer;
    searchnum, result :integer;

procedure binarySearch(left, right :integer);
var
    middle : integer;
begin
    if left <= right then
        begin
            middle := (left + right) div 2;
            if (a[middle] > searchnum) then
                binarySearch(left, middle - 1)
            else if (a[middle] < searchnum) then
                binarySearch(middle + 1, right)
            else
                result := middle;
        end
    else
        result := -1;
end;

参考资料

  1. Yan, Weimin., Wu, Weimin. 数据结构: C语言版. China: 清华大学出版社, 1997.《数据结构基础（C语言版）》第二版
  2. 二分搜索算法 - 维基百科，自由的百科全书